Transfomer（Attention is all you need）

• 序列转入模型：给出一个序列，生成另外一个序列。（机器翻译）CNN、RNN、encoder and a decoder

• 亮点：仅仅依赖于注意力机制，没有RNN或者CNN

• RNN
  • 缺点
    • 运算中无法并行，计算$h_{t}$需要$h_{t-1}$的信息
    • 序列太长，会丢失早期的时序信息

1. encoder-decoder

• encoder：将输入转变为机器能够理解的向量。$X=(x _1,…,x _n)$转变为$Z=(z _1,…,z _n)$
  • LayerNorm(x + Sublayer(x))
    • batchNorm：假设输入为二维矩阵（batch，feature），每次将每一列（特征）的数据变为均值为0、方差为1（向量减去其均值然后除以方差）
    • LayerNorm：假设输入为二维矩阵（batch，feature），每次将每一行（样本）的数据变为均值为0、方差为1（向量减去其均值然后除以方差）
  • Sublayer：Muti-head Attention - Feed Forward
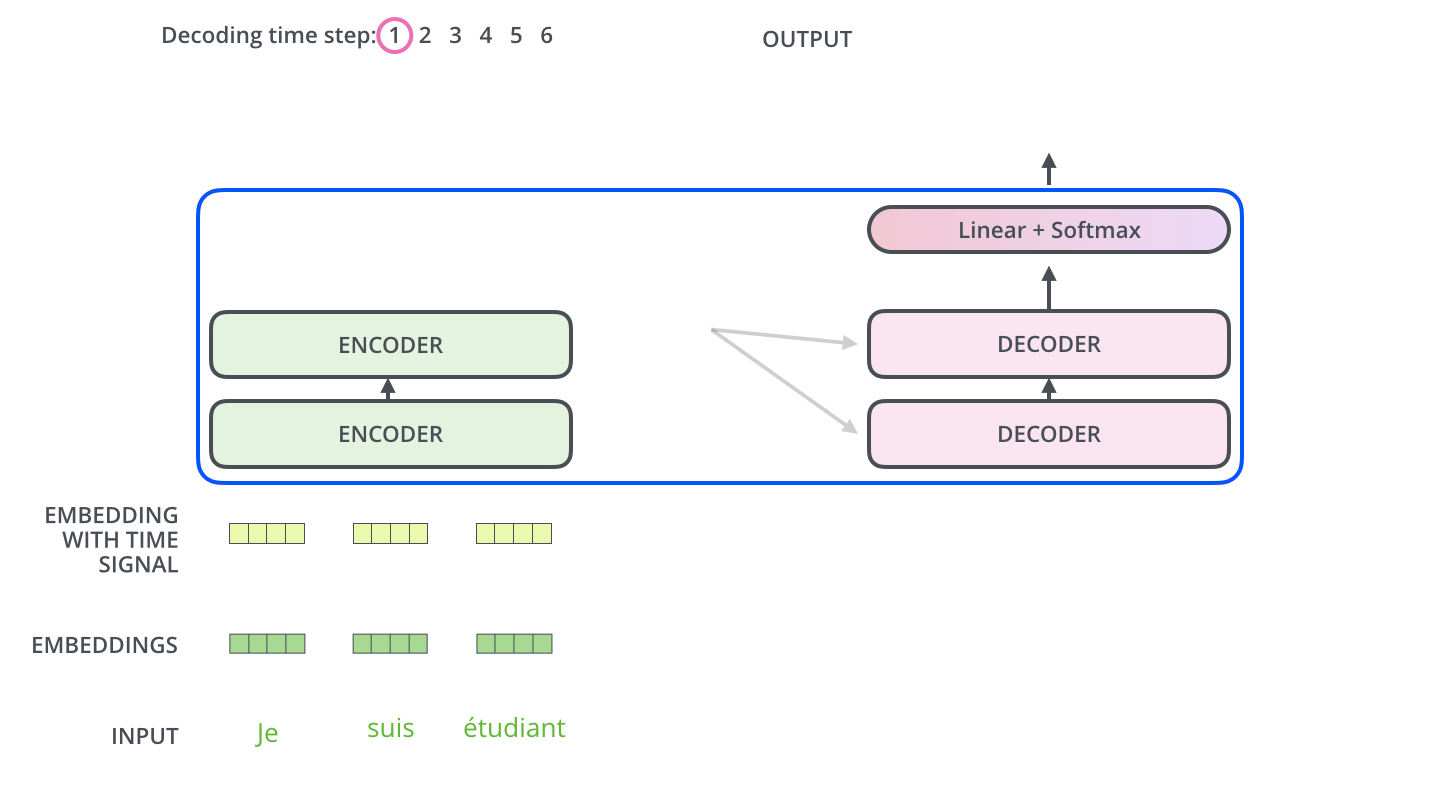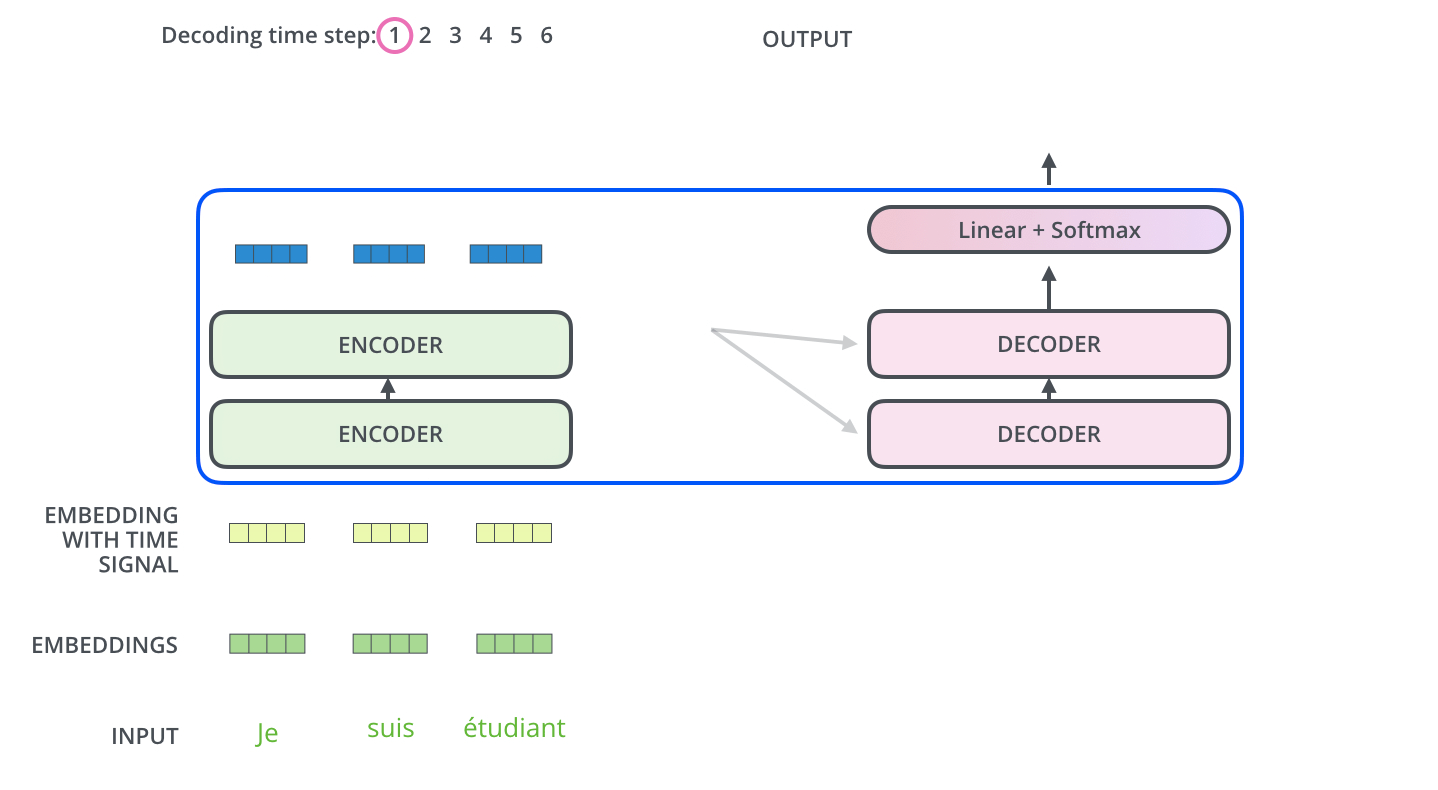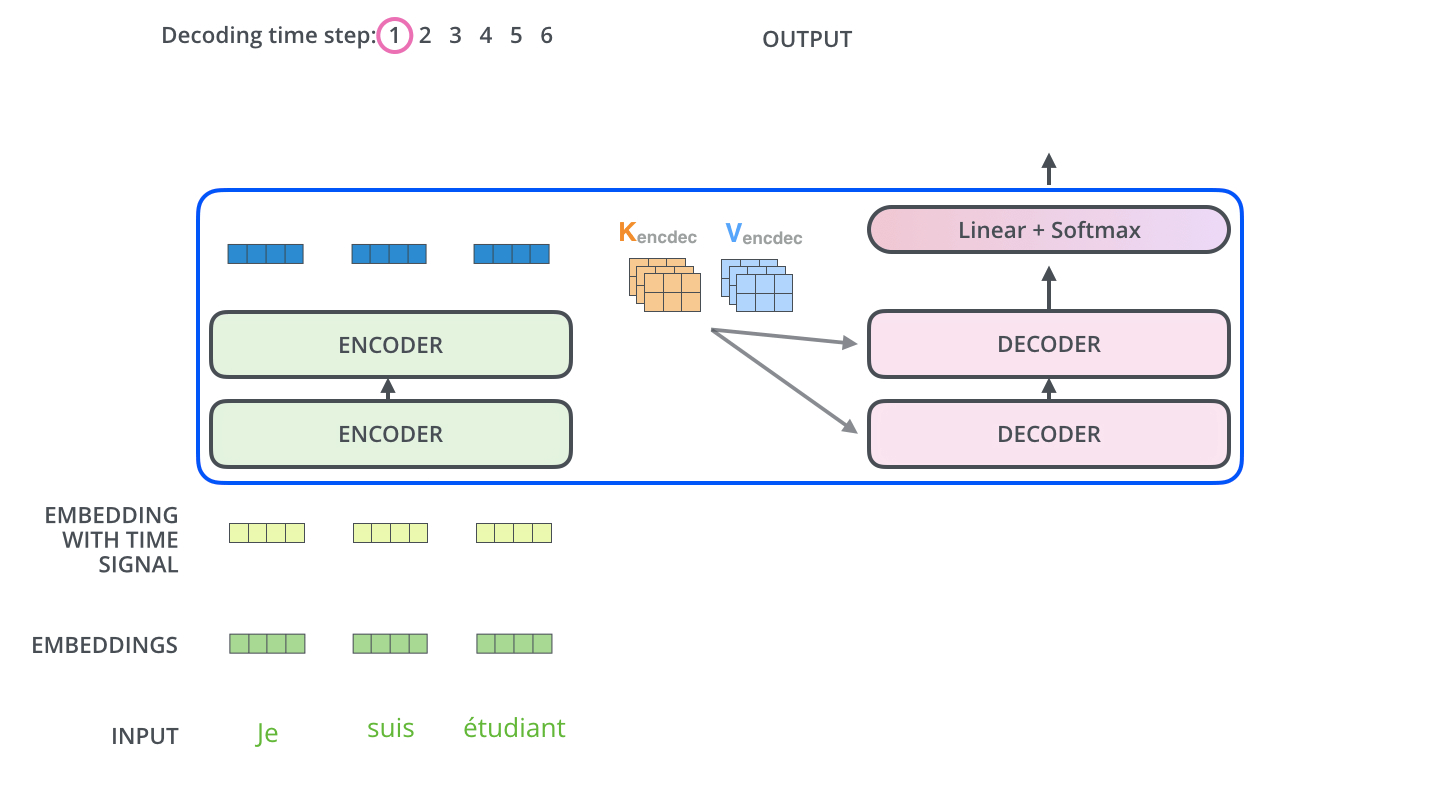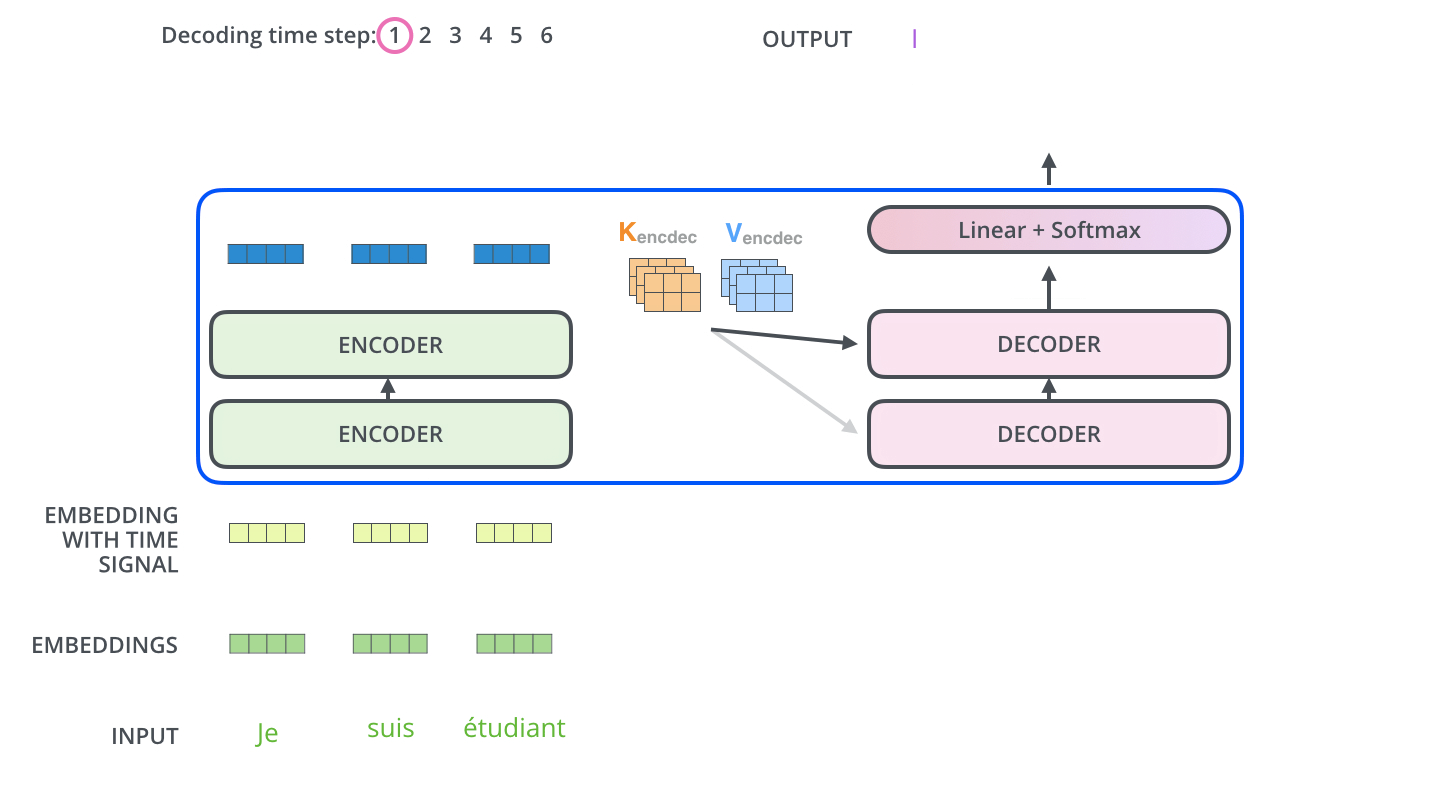
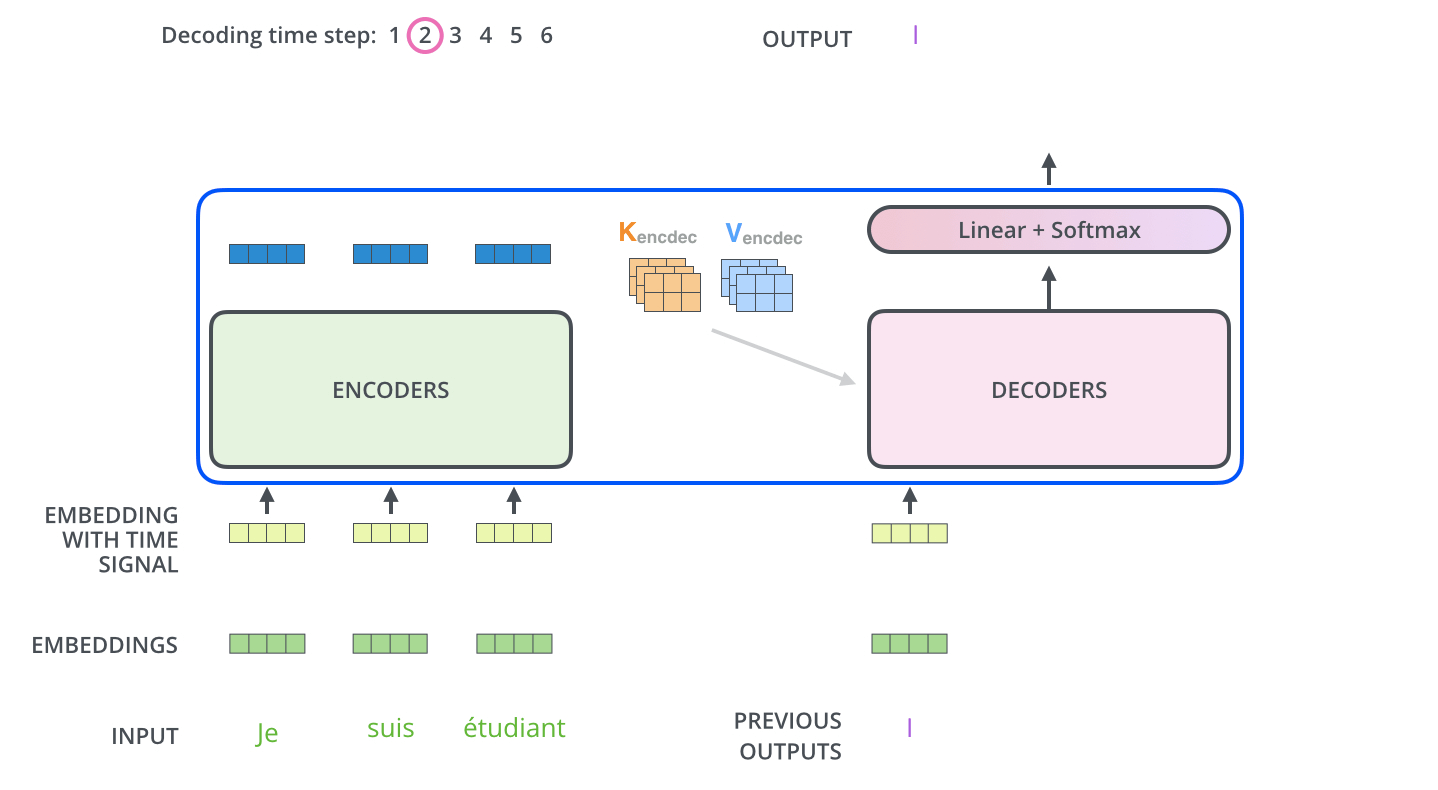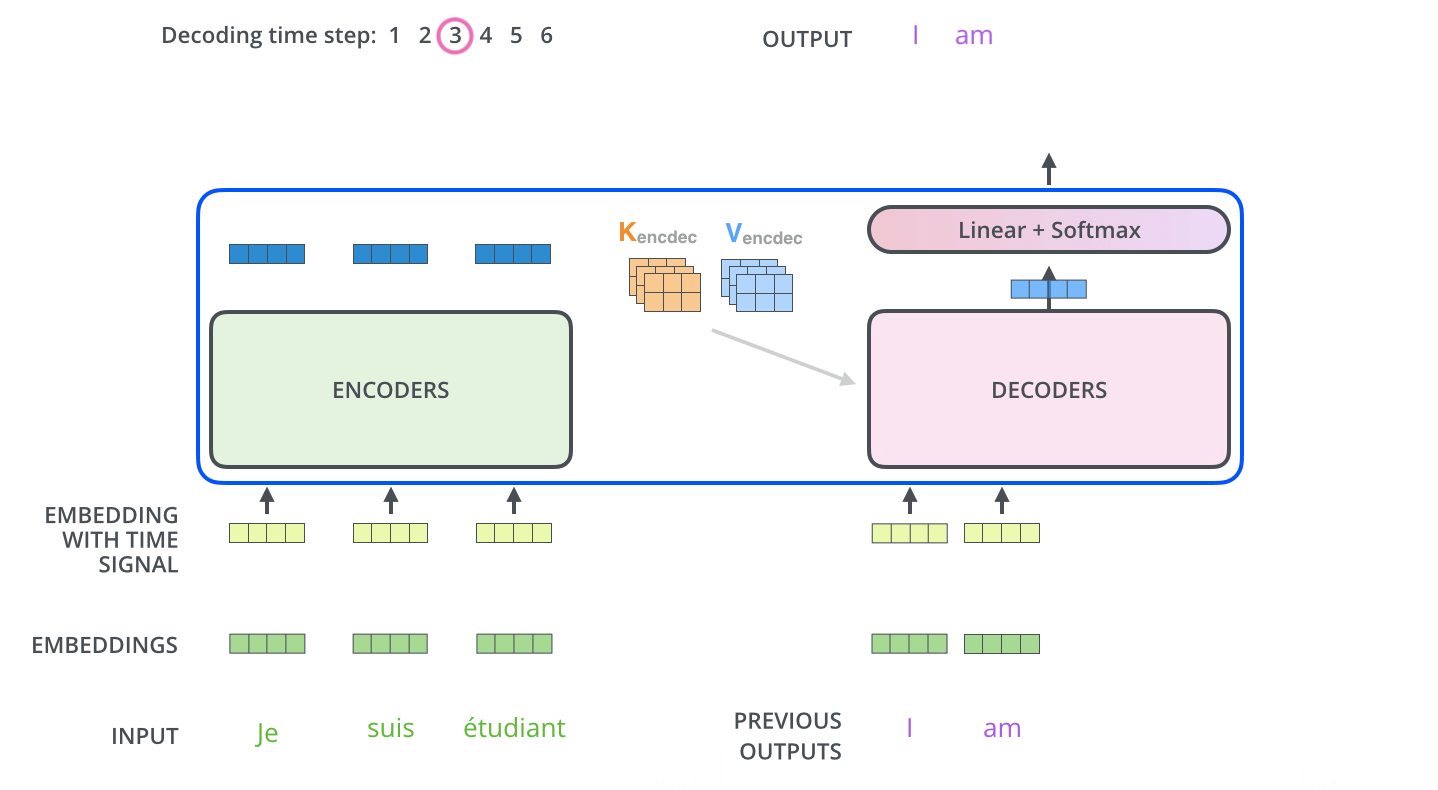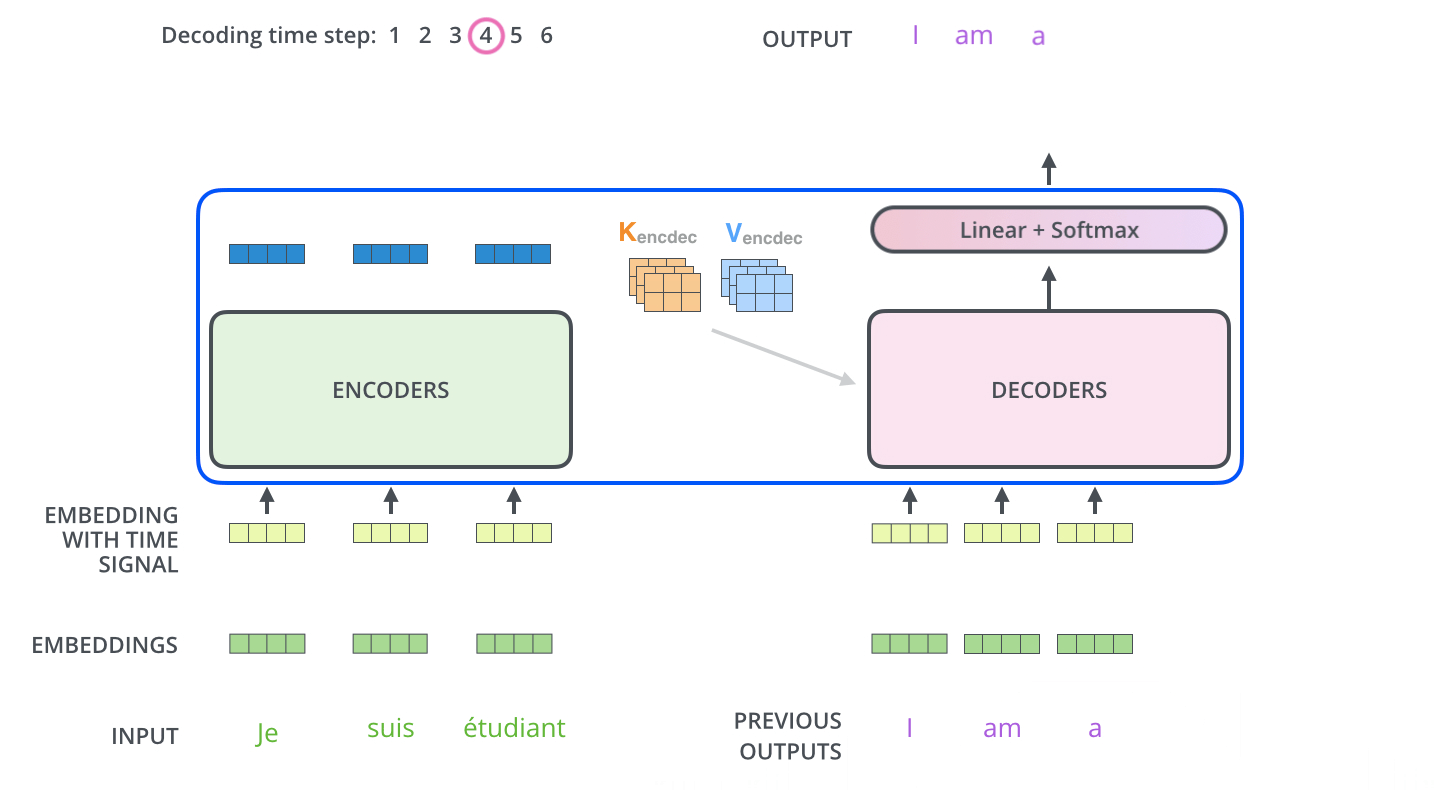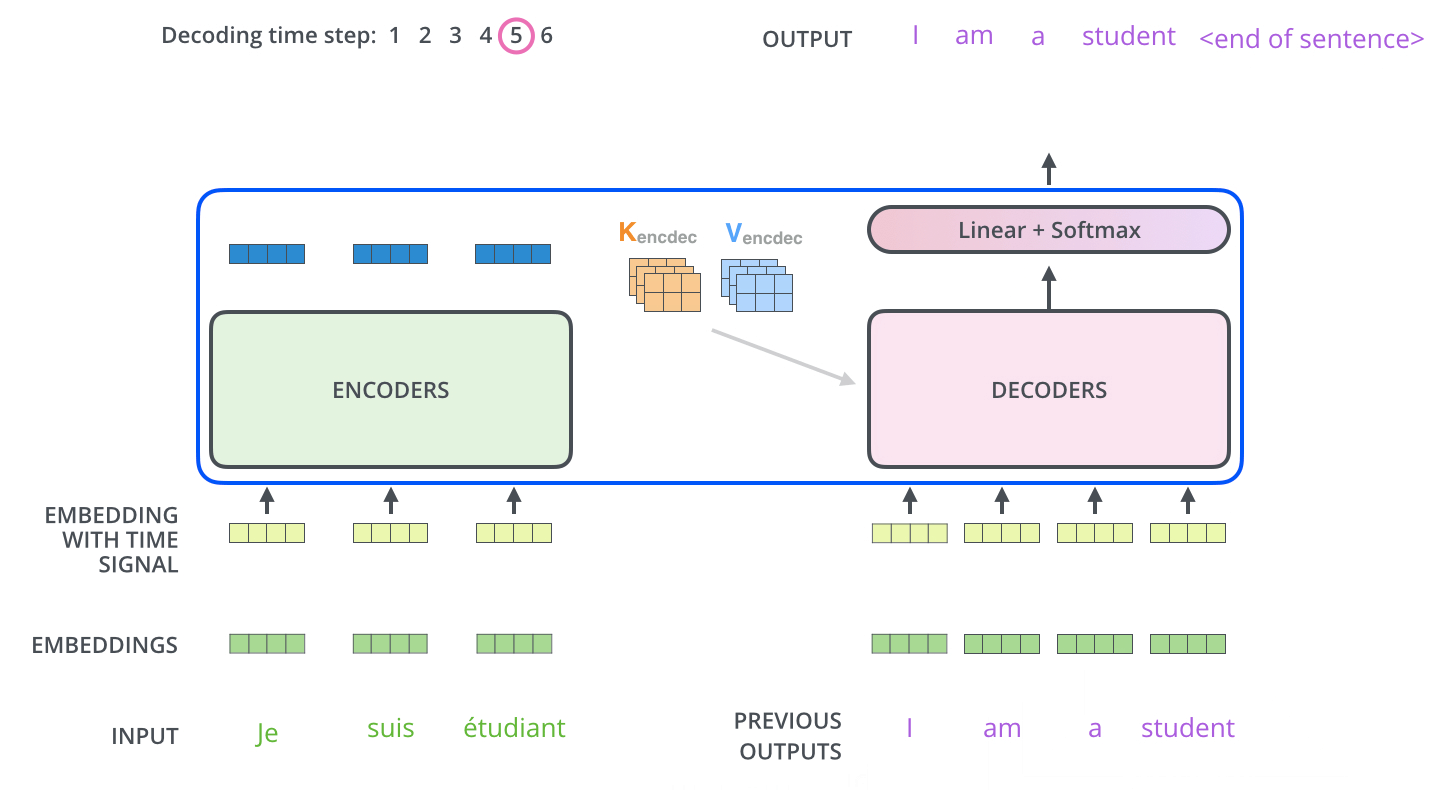
• decoder：由$Z=(z _1,…,z _n)$得到$Y=(y _1,…,y _m)$
• 区别：在decoder中，字是一个一个生成的，称为自回归（过去时刻的输出作为当前时刻的输入）

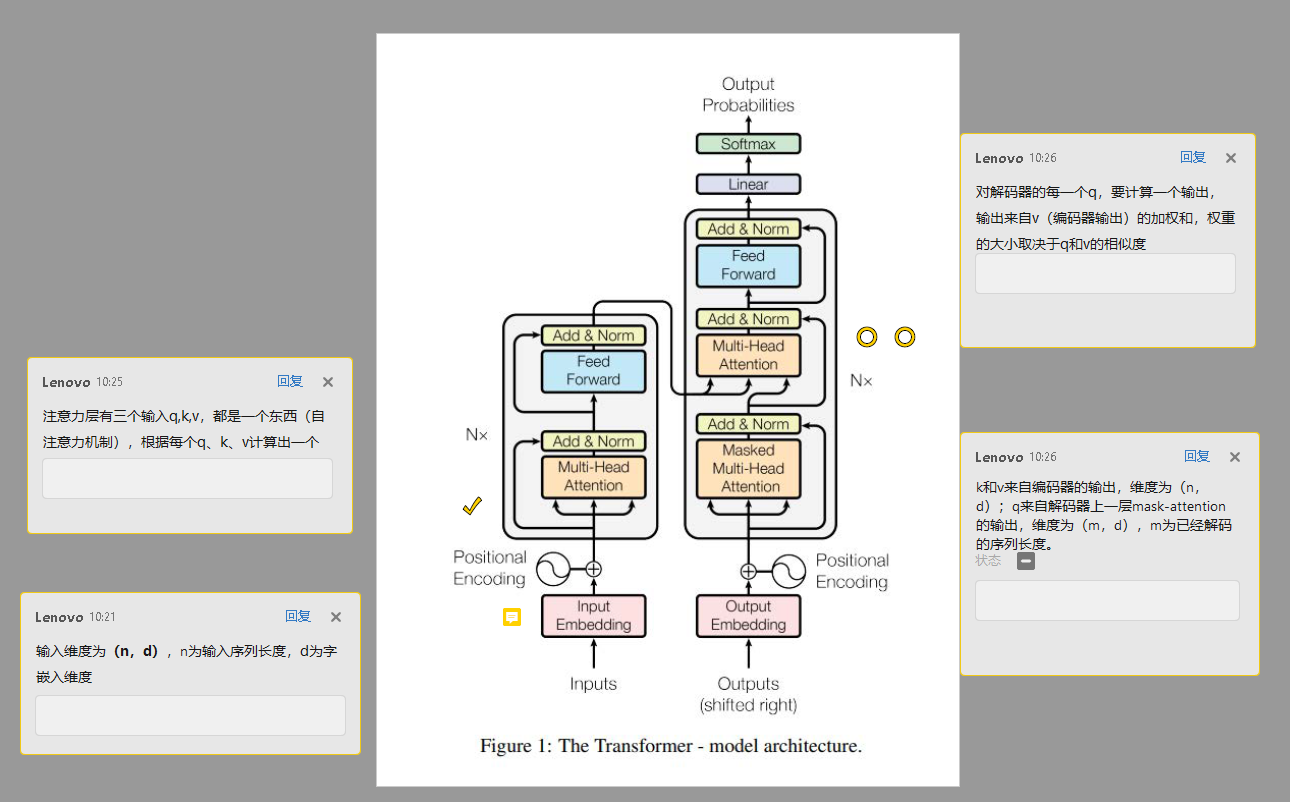
2. encoder-decoder图示

• 文本向量化

  将每个单词都嵌入到512维的向量中

  

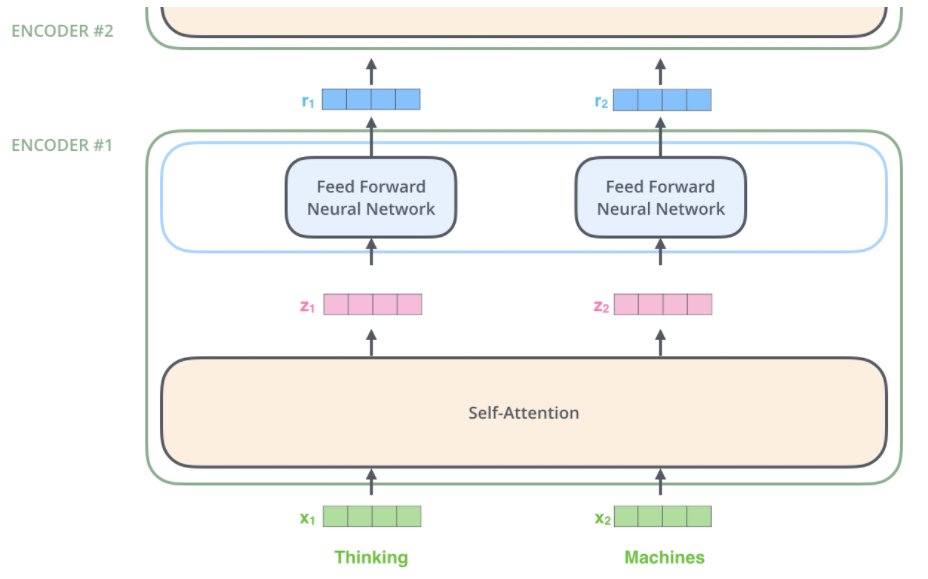
• 编码器

  编码器接受上面的向量列表作为输入，首先通过自注意力层，然后进行残差连接和LayerNorm，最后通过前馈神经网络层。编码器的输出作为下一个编码器的输入，嵌套n个编码器。

  

  动图演示：

  

• 解码器

  

3. 技术细节描述

3.1 Self-attention计算流程

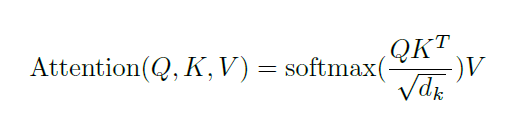
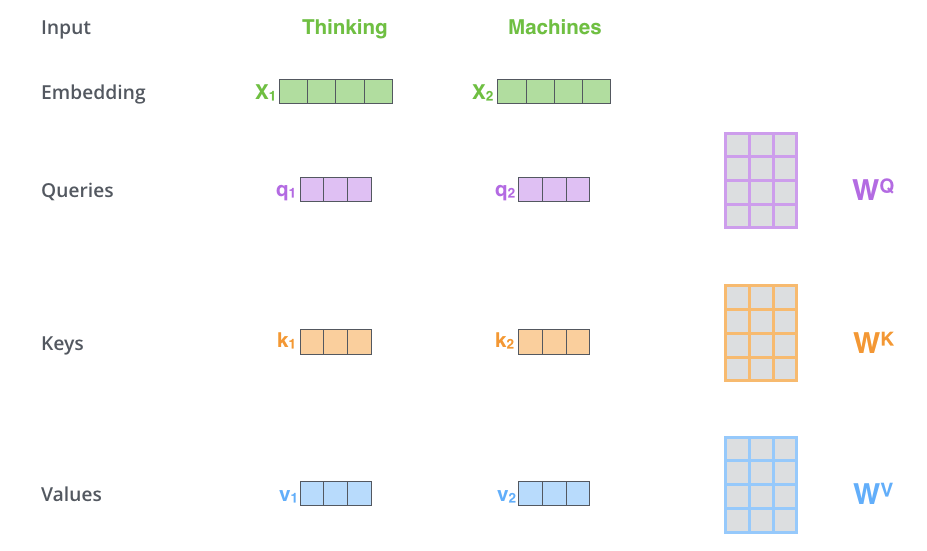
• 生成计算向量矩阵

  • 根据每个字嵌入向量构建三个向量矩阵，分别为Q、K、V，嵌入字向量的维度为512维，因此Q，K，V的维度为（512/num_head）

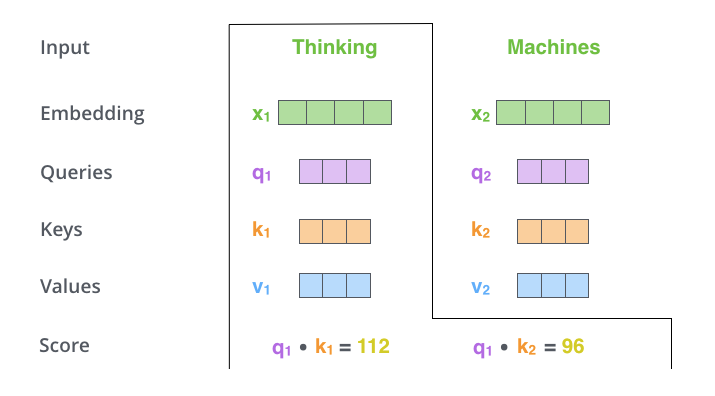
• 计算自注意力分数（以单词“Thinking”为例）

  • 自注意力分数决定了在某个位置对单词进行编码时，将多少注意力放在输入句子的其他部分上

  • 计算Q和K的内积（内积的值越大，向量之间的相似度越高），q和每个k做内积

    

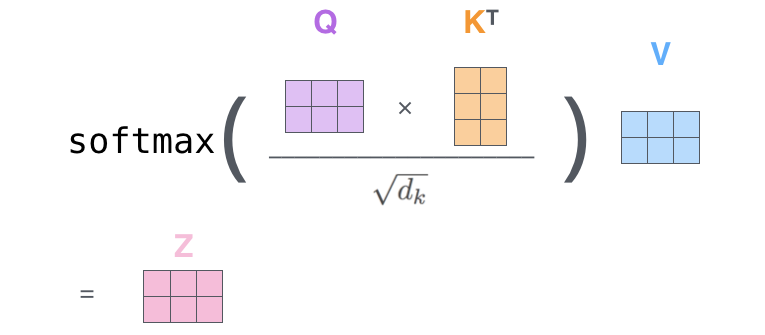
  • 除以$\sqrt{d _{k}}$ （向量的长度），用softmax函数得到每个k对应的权重（非负，加起来和为1），value乘以权重得到最后的输出

3.2 Self-attention矩阵运算

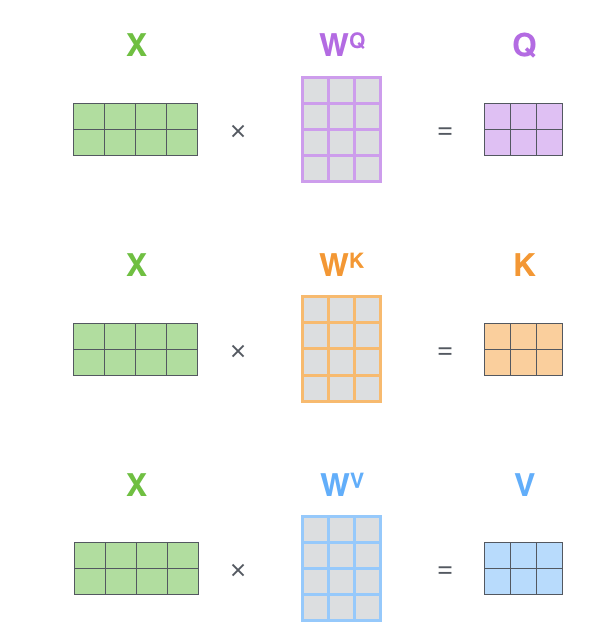
• 第一步，计算Q、K、V矩阵

• 第二步，批量计算自注意力值

  

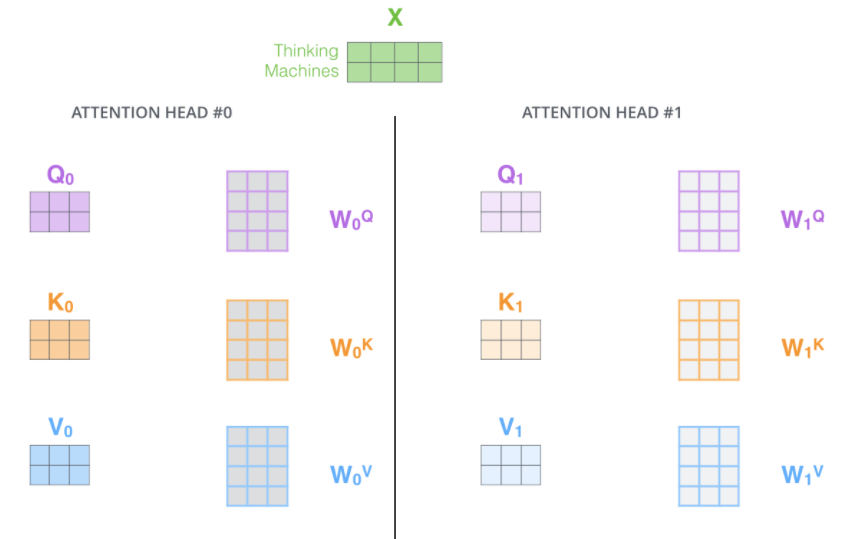
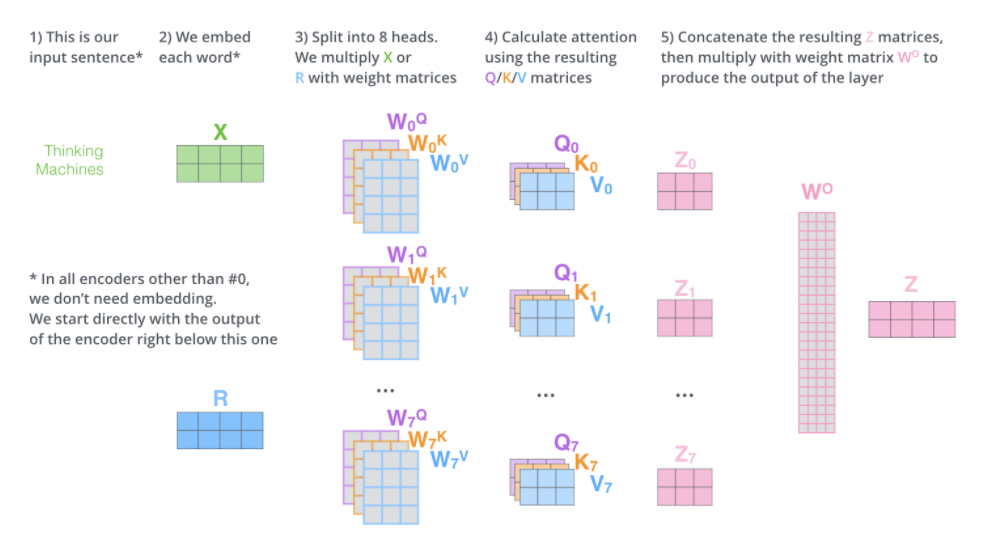
3.3 Muti-head self attention

• 优点

  • 拓展了模型专注于不同位置的能力
  • 为注意力层提供了多个“表示子空间”，n个head则提供了n组Q、K、V查询矩阵，这些矩阵向量是随机初始化的，将输入嵌入投影到不同的表示子空间中

• 第一步，对每组不同的Q、K、V查询矩阵进行运算，得到对应的Q、K、V矩阵

  

• 第二步，使用n个不同的Q、K、V权重矩阵进行自注意力计算，得到n个不同的Z矩阵

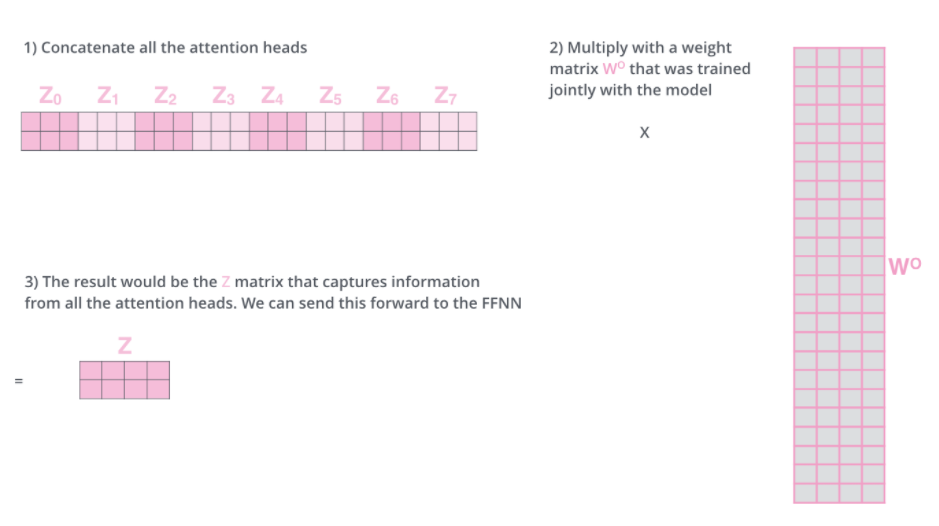
  • 但是前馈神经网络层并不需要八个矩阵，它只需要一个矩阵（每个单词一个向量），因此需要将这个八个矩阵压缩为一个矩阵

  • 方法：使用一个额外的权重矩阵将他们相乘，得到最终的矩阵输出

    

• 总体流程

  

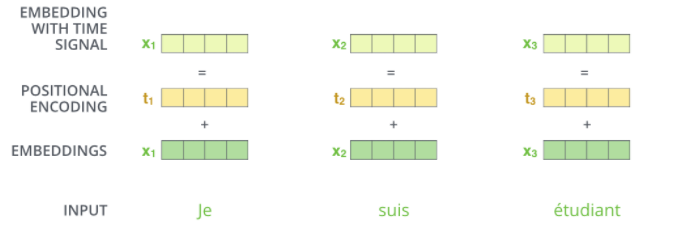
3.4 Position embedding

模型需要编码序列中单词的顺序，transfomer为每个输入嵌入增加了一个向量。这些向量遵循模型学习的特定模式，有助于确定每个单词的位置，或序列中不同单词之间的距离。

• 直观图

  

3.5 Residual connection

每个编码器中的每个子层周围都有一个残差连接，然后是层归一化步骤。

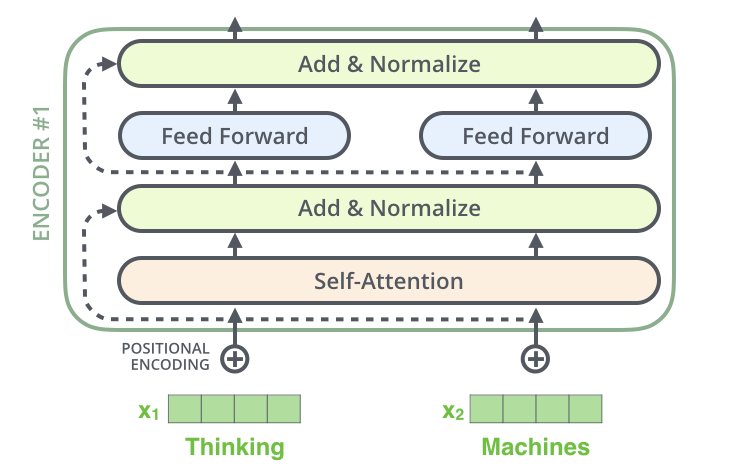
具体可视化如下：

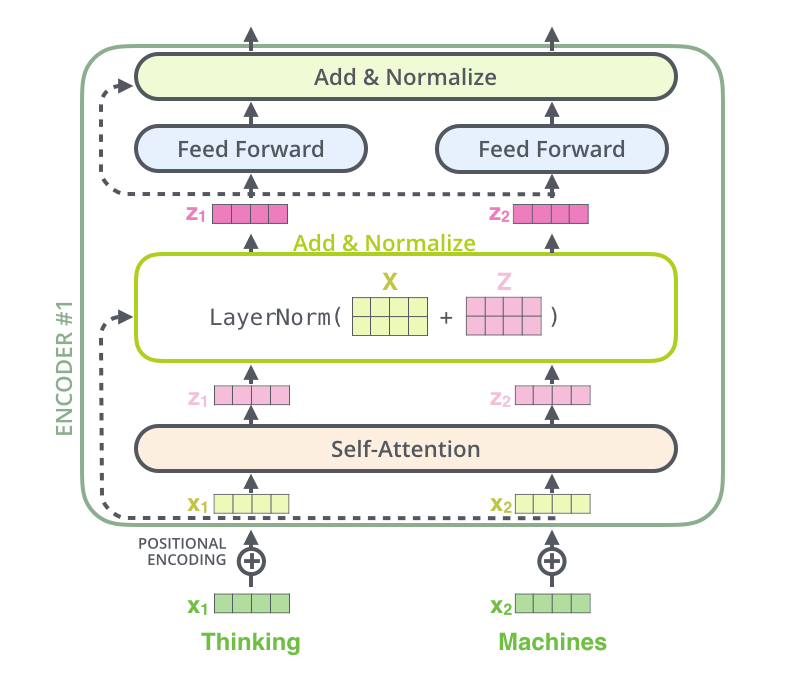
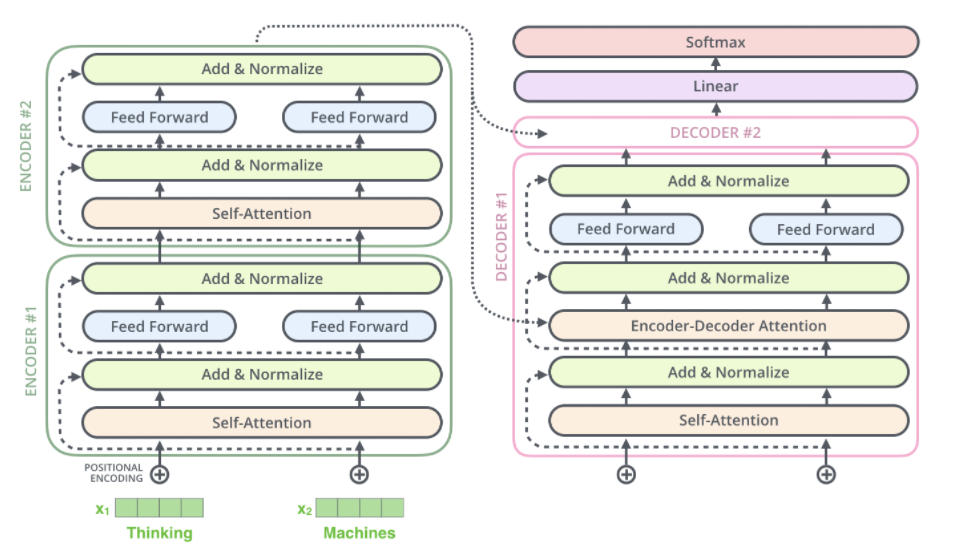
全局可视化如下：

3.6 Final Linear and Softmax Layer

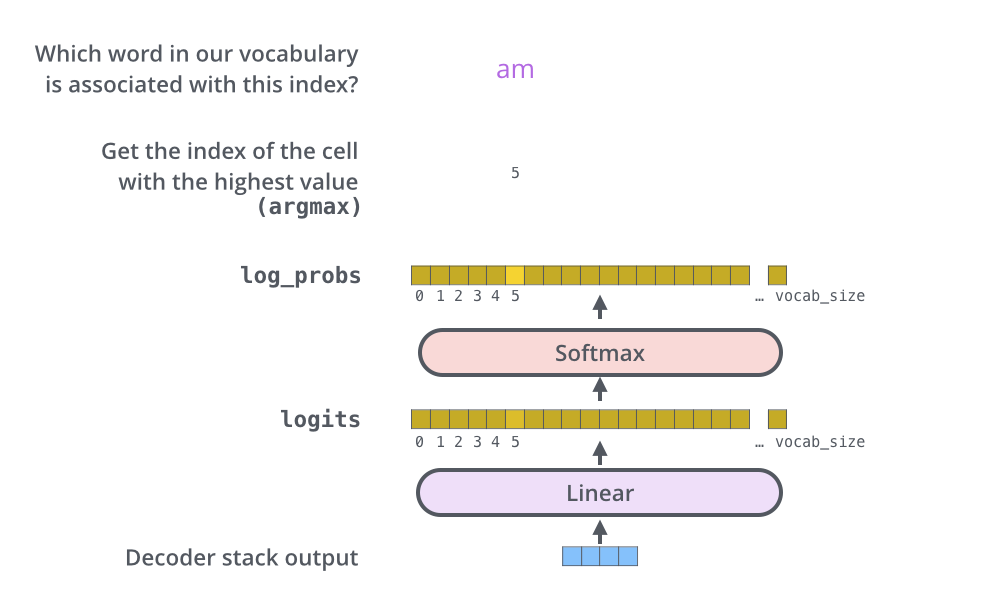
• 将解码器输出的向量通过线性层映射到n_word维的向量空间，n_word为字典中词汇数量。
• 然后将这个n_word维的向量通过softmax层映射为每个词汇的概率，最后选择概率最高的关联词汇作为该时间步的输出。